|
|
| Menu: Edit Object - Boolean Operation
|
|
|
|
|
|
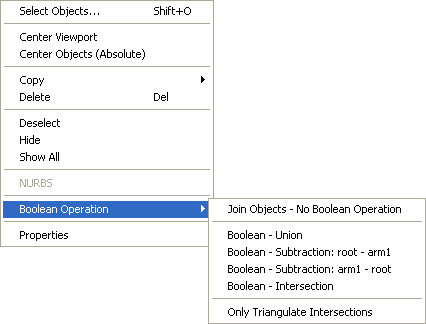
| If you choose the <Boolean Operation> button in the "Edit Object" tool-window, a popup selection opens with several entries for joining objects in different ways. Those entries are found also in the popup selection, which opens when clicking with the right mouse button in a viewport window (see picture above) and again in the "Object Selection" dialog, thus enabling access to these functions in every work mode.
|
|
|
| A Boolean Operation (named after the English mathematician George Boole) describes the connection of 2 objects with simple logical operators like "AND" or "OR". CyberMotion makes use of this logic when joining two overlapping, facet based objects, which results in complex structures that otherwise would be very difficult to construct. For instance, it is very easy to add a hole to an object, just by placing a cylinder at the desired position for the hole and then operate a Boolean Subtraction "object" minus "cylinder".
|
|
|
| To apply a Boolean Operation, first mark the two overlapping, facet-based objects. Analytical objects and NURBS cannot be joined, but you can convert NURBS to facet-based objects and after that a Boolean Operation will be possible. When a Boolean Subtraction is applied, the resulting object will adopt the name, material and animation data of the object from which you subtract the other object. Otherwise the data is adopted from the selected reference object. If neither of the two marked objects is selected as a reference object, than the data of the object located higher in the hierarchy list will be used.
|
|
|
| Functions:
|
| · | Join Objects - No Boolean Operation
|
| · | Boolean Union
|
| · | Boolean Subtraction
|
| · | Boolean Intersection
|
| · | Problems using Boolean Operations
|
| · | Only Triangulate Intersection
|
|
|
| This function merely serves to manage 2 objects as one object. In many cases it is simpler to manipulate objects that are composed of many different parts (but of the same material) as a single object - as you continually save yourself work on processing a group object. The object construction itself remains unchanged. No Boolean Operation is applied - just 2 objects being referenced as one single object.
|
|
|
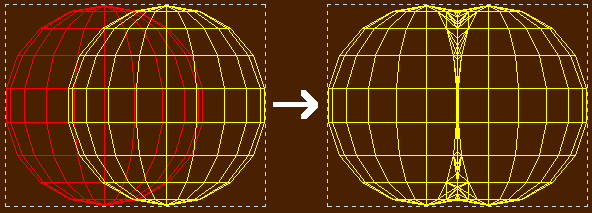
| The Boolean Union function combines 2 objects by way that removes all facets and points of each object that lie completely within the other object. In the process, the overlapping facets will be subdivided along their intersecting edges to create a seamless transition along the overlapping objects.
|
|
| This is best shown in wire frame mode. Two overlapping spheres are melded with a Boolean Union operation. The superfluous inner parts were eliminated and the additionally generated facets and points for the joining edges are clearly visible.
|
|
|

|
| The Boolean Subtraction uses one object as a tool to cut a shape from the other object. Above you see an example for an operation "Box" minus "Torus".
|
|
|

|
| This operation is not restricted to simple primitive shapes, even complex structures can be combined. The picture shows a Boolean Subtraction of a 3D text object "e" from a "box". However, because of the intensive calculation process you should keep objects as simple as possible. If, for example, you want to subtract a complete text string of high resolution 3D text from a box, I would recommend to do this character by character and afterwards join the separate objects.
|
|
|

|
| Another example of use is to produce cross-sections of objects. In the picture you can see a primitive object "box" that was subtracted from a "Torus", so that the "Torus" was cut into two parts. The points of one half of the "Torus" were then selected and transformed into an independent object by means of the Detach Object function.
|
|
|

|
| A Boolean Intersection calculates a new object from the intersecting parts of the two objects.
|
|
|
| When calculating a Boolean Operation there is one basic problem - to determine which facets or points of an object lie inside or outside the other object.
|
| With primitive convex objects this is very easy, but with non-convex objects calculations can go to great lengths.
|
| Although Boolean Operations are intended to be for objects with closed surfaces - since only then you can determine exactly, which parts of an object lie inside the other object - you can also apply Boolean Operations to open objects. One criterion, whether a point lies inside or outside, is to check if the point is located underneath a surface facet of the other object. This can be calculated from the facet's normal (a vector standing vertical to the surface). With closed objects this surface normals always point to the outside, but with open objects it depends on the view of the user, what is intended to be inside or outside.
|
| If the result of a Boolean Operation with an open object is unsatisfying, you can try to repeat the operation after inverting the normals of the object.
|

|
| The picture shows a box with an open front. A cone is to be subtracted from the box to create a funnel opening. But the operation results only in an undesirable hole.
|

|
| This shows the same situation except that we have inverted the normals of the box before applying the Boolean Subtraction. Now it worked out well and the funnel was inset into the box.
|
|
|
| This function is the preliminary stage for all Boolean Operations. The process subdivides the overlapping facets along their intersecting edges to create a seamless transition along the overlapping objects. But after applying this function no Boolean Operation is executed, thus enabling the user to select by hand the points and facets he wants to delete. Afterwards the objects can be joined again using the "Join Objects" function.
|


